Exercices
Chapitre 1: Algorithmes sur les arbres binaires
1 Implémentations des algorithmes du cours
En utilisant le module binarytree, implémenter les algorithmes du programme officiel:
Calculer la hauteur de l’arbre
Calculer la taille de l’arbre
Parcours de l’arbre
- Parcours préfixe
- Parcours postfixe
- Parcours infixe
- Parcours en largeur
Arbre binaire de recherche
- Insertion d’une clé
- Recherche d’une clé
Pour le parcours en largeur, on pourra utiliser la classe File suivante.
2 Version itérative des parcours en profondeur
Il est possible d’écrire des versions iteratives (et non récursive) des algorithmes de parcours en profondeur.
Pour cela on utilisera une pile(stack en anglais).
Voici les pseudo-codes proposés sur l’article Wikipédia en anglais.
2.1 Parcours préfixe itératif
iterativePreorder(node)
if (node == null)
return
s ← empty stack
s.push(node)
while (not s.isEmpty())
node ← s.pop()
visit(node)
//right child is pushed first so that left is processed first
if node.right ≠ null
s.push(node.right)
if node.left ≠ null
s.push(node.left)2.2 Parcours infixe itératif
iterativeInorder(node)
s ← empty stack
while (not s.isEmpty() or node ≠ null)
if (node ≠ null)
s.push(node)
node ← node.left
else
node ← s.pop()
visit(node)
node ← node.right2.3 Parcours postfixe itératif
iterativePostorder(node)
s ← empty stack
lastNodeVisited ← null
while (not s.isEmpty() or node ≠ null)
if (node ≠ null)
s.push(node)
node ← node.left
else
peekNode ← s.peek()
// if right child exists and traversing node
// from left child, then move right
if (peekNode.right ≠ null and lastNodeVisited ≠ peekNode.right)
node ← peekNode.right
else
visit(peekNode)
lastNodeVisited ← s.pop()Pour faire cet exercice, on pourra utiliser la classe Pile suivante.
3 Un arbre de compétition (d’après BAC 2021)
La fédération de badminton souhaite gérer ses compétitions à l’aide d’un logiciel. Pour ce faire, une structure arbre de compétition a été définie récursivement de la façon suivante: un arbre de compétition est soit l’arbre vide, noté ∅, soit un triplet composé d’une chaîne de caractères appelée valeur, d’un arbre de compétition appelé sous-arbre gauche et d’un arbre de compétition appelé sous-arbre droit.
- On considère l’arbre de compétition
Bsuivant:
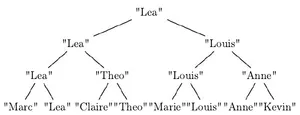
Créer l’arbre de compétition B à l’aide de la classe ArbreBinaire vue dans le chapitre P1C4.
Écrire les fonctions suivantes:
- La fonction
racinequi prend en paramètre un arbre de compétitionarbet renvoie la valeur de la racine.
- La fonction
Exemple: en reprenant l’exemple d’arbre de compétition présenté ci-dessus, racine(B) vaut "Lea".
La fonction
gauchequi prend en paramètre un arbre de compétitionarbet renvoie son sous-arbre gauche.La fonction
droitqui prend en argument un arbre de compétitionarbet renvoie son sous-arbre droit.La fonction
est_videqui prend en argument un arbre de compétition et renvoieTruesi l’arbre est vide etFalsesinon.Exemple:en reprenant l’exemple d’arbre de compétition présenté ci-dessus,
est_vide(B)vautFalse.
** Dans toute la suite de l’exercice, vous ne devrez utiliser que les fonctions définies dans les questions précédent la question posée.**
Proposer une fonction Python
occurrencesayant pour paramètre un arbre de compétitionarbet le nom d’un joueurnomet qui renvoie le nombre d’occurrences (d’apparitions) du joueurnomdans l’arbre de compétitionarb.Exemple:
occurences(B,"Anne")vaut2.Proposer une fonction Python
a_gagneprenant pour paramètres un arbre de compétitionarbet le nom d’un joueurnomet qui renvoie le booléenTruesi le joueurnoma gagné au moins un match dans la compétition représenté par l’arbre de compétitionarb.Exemple:
a_gagne(B,"Louis")vaut True
On souhaite programmer une fonction Python
nombre_matchsqui prend pour arguments un arbre de compétitionarbet le nom d’un joueurnomet qui renvoie le nombre de matchs joués par le joueurnomdans la compétition représentée par l’arbre de compétitionarbExemple:
nombre_matchs(B,"Lea")doit valoir3etnombre_matchs(B,"Marc")doit valoir1.Expliquer pourquoi les instructions suivantes renvoient une valeur erronée. On pourra pour cela identifier le nœud de l’arbre qui provoque une erreur.
Proposer une correction pour la fonction
nombre_matchs.
Recopier et compléter la fonction
liste_joueursqui prend pour argument un arbre de compétitionarbet qui renvoie un tableau contenant les participants au tournoi, chaque nom ne devant figurer qu’une seule fois dans le tableau.L’opération
+à la ligne 8 permet de concaténer deux tableaux.Exemple: Si
L1 = [4, 6, 2]etL2 = [3 ,5 ,1 ], l’instructionL1 + L2va renvoyer le tableau[4, 6, 2, 3, 5, 1]