Chapitre 4: Arbres

Programme

Contenus	Capacités attendues	Commentaires
Arbres : structures hiérarchiques. Arbres binaires : nœuds, racines, feuilles, sous-arbres gauches, sous-arbres droits.	Identifier des situations nécessitant une structure de données arborescente. Évaluer quelques mesures des arbres binaires (taille, encadrement de la hauteur, etc.).	On fait le lien avec la rubrique « algorithmique ».

Arbres : structures hiérarchiques.

Arbres binaires : nœuds, racines, feuilles, sous-arbres gauches, sous-arbres droits.

Identifier des situations nécessitant une structure de données arborescente.

Évaluer quelques mesures des arbres binaires (taille, encadrement de la hauteur, etc.).

On fait le lien avec la rubrique « algorithmique ».

By ‍Birger Eriksson - Own work, CC BY-SA 3.0, Link

Dans ce chapitre, on présente une nouvelle structure de donnée: les arbres qui sont particulièrement adaptés à la représentation des données hiérarchiques comme un arbre généalogique ou encore le DOM d’une page html.

1 Vocabulaire

Arbre: Un arbre est constitué de nœuds reliés par des arêtes. Souvent les nœuds ont une valeur: l’étiquette.
Racine d’un arbre enraciné: Un arbre enraciné (ou arborescence) possède à sa base une racine auxquels sont reliés d’autres nœuds qui sont ses descendants.

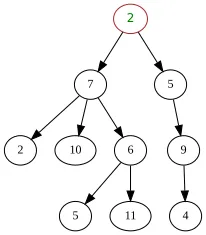
Dans cet arbre, la racine est le noeud 2 au sommet coloré en vert.

Un nœud situé à l’extrémité de l’arbre qui n’a donc pas de descendants est une feuille.

Chaque nœud peut avoir un nombre quelconque de nœuds fils, mais il n’a qu’un nœud père (sauf la racine qui n’a pas de nœud père).

Profondeur d’un nœud: La profondeur d’un nœud est la distance, c’est-à-dire, le nombre d’arêtes de la racine au nœud.
Hauteur d’un arbre: La hauteur d’un arbre est la plus grande profondeur d’une feuille de l’arbre.
Taille d’un arbre: La taille d’un arbre est son nombre de nœuds.

Application

Reproduire l’arbre ci-dessus, et l’annoter en légendant:

la racine,
des feuilles,
un nœud père et ses fils.

Calculer la hauteur et la taille de cet arbre.

2 Arbres binaires

2.1 Définition

Arbre binaire: Les arbres binaires sont un type d’arbres particuliers pour lesquels chaque nœud a au plus deux fils.

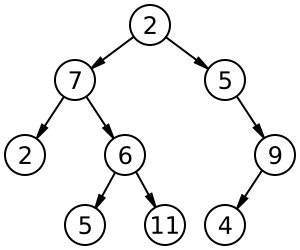
Dans un arbre binaire, un noeud ne peut avoir plus de 2 enfants.

2.2 Implémentation récursive

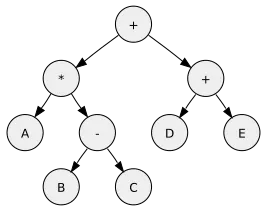
Comme chaque nœud d’un arbre binaire a au plus deux enfants, on définit les sous arbres gauche et sous arbre droit d’un nœud.

CC-BY-SA David Roche

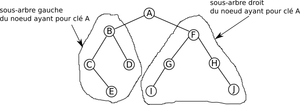
Un arbre binaire est une structure de données récursive. Tout nœud d’un arbre binaire est un arbre binaire.

On peut ainsi définir une classe ArbreBinaire récursive comme suit:

# nécessaire pour pouvoir annoter le type de la classe
from __future__ import annotations


class ArbreBinaire:
    """Structure de donnée d'arbre binaire"""

    def __init__(self, étiquette: str, gauche: ArbreBinaire, droit: ArbreBinaire):
        self.étiquette = étiquette
        self.gauche = gauche
        self.droit = droit

Application

Écrire la séquence d’instructions permettant de construire l’arbre binaire présenté en exemple ci-dessus.
Expliquer comment accéder à l’étiquette du nœud 7(en partant de la racine) à partir de cette implémentation.

2.3 Parcours d’un arbre binaire

Il existe diverses façons de parcourir les nœuds d’un arbre.

Le parcours en largeur d’abord: les nœuds sont parcourus comme si on lisait l’arbre, de haut en bas et de gauche à droite.

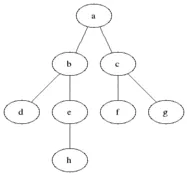
Le parcours en profondeur d’abord: on explore complétement le sous-arbre gauche avant de commencer l’exploration du droit. Il existe trois façons de faire:

Parcours préfixe ou préordre (NGD): on visite d’abord le nœud, puis son sous-arbre gauche, puis son sous-arbre droit.
Parcours infixe ou en ordre (GND): on visite d’abord le sous-arbre gauche, puis le nœud, puis le sous-arbre droit.
Parcours postfixe ou en postordre (GDN): on visite d’abord le sous-arbre gauche, puis le sous-arbre droit, et enfin le nœud.

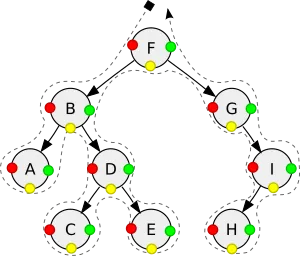
Parcours en profondeur d’abord d’un exemple d’arbre:

préfixe (rouge): F, B, A, D, C, E, G, I, H;
infixe (jaune): A, B, C, D, E, F, G, H, I;
postfixe (vert): A, C, E, D, B, H, I, G, F.

Les trois ordres possibles de parcours en profondeur.

Application

Donner les quatre ordres de parcours de l’arbre ci-dessous qui représente une expression arithmétique.

Quel parcours représente la notation habituelle de nos calculatrices actuelles?

3 Arbres binaires de recherche

3.1 Définition

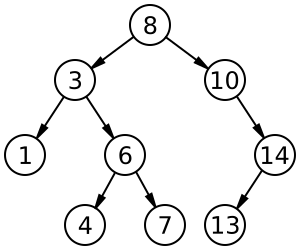
Arbre binaire de recherche: Il s’agit d’un arbre binaire dans lequel toutes les valeurs dans le sous-arbre gauche d’un nœud sont inférieures à la valeur à la racine de l’arbre et toutes les valeurs dans le sous-arbre droit d’un nœud sont supérieures ou égales à la valeur à la racine de l’arbre.

Un arbre binaire de recherche est l'équivalent d'une liste triée pour les arbres binaire, ils permettent des recherches très efficaces.

Application

Proposer deux arbres binaires de recherche avec tous les entiers entre 1 et 6 dont l’un est complet(tous les étages sont entièrement remplis, sauf le dernier ou les feuilles sont tassées à gauche).
Proposer deux arbres binaires de recherche avec tous les entiers entre 1 et 15 dont l’un est parfait(tous les étages sont entièrement remplis).

3.2 Implémentation en P.O.O.

Dans un arbre binaire de recherche, les nœuds ne peuvent pas être placés n’importe comment et doivent respecter l’ordre entre les sous arbres et le nœud: $G<N<D$ .

On peut créer une classe ABR semblable à la classe ArbreBinaire, mais en lui ajoutant une méthode insérer pour ajouter l’élément à sa place dans l’arbre binaire de recherche.

On peut ainsi définir une classe ArbreBinaire récursive comme suit:

# nécessaire pour pouvoir annoter le type de la classe
from __future__ import annotations


class ABR:
    """Structure de donnée d'arbre binaire de recherche"""

    def __init__(self, étiquette: int, gauche: ABR, droit: ABR):
        self.étiquette = étiquette
        self.gauche = gauche
        self.droit = droit

    def insérer(self, valeur):
        """Insère une valeur à sa place dans l'arbre"""

        # si la valeur est inférieure on l'insère à gauche
        if valeur < self.étiquette:
            # si il y a pas de noeud à gauche, on l'insère
            if self.gauche is None:
                self.gauche = ABR(valeur, None, None)
            # sinon on fait un appel récursif sur le sous arbre gauche
            else:
                self.gauche.insérer(valeur)
        else:
            if self.droit is None:
                self.droit = ABR(valeur, None, None)
            else:
                self.droit.insérer(valeur)

Application

À quoi ressemblerait l’arbre créé en insérant successivement tous les entiers entre 1 et 6 comme ceci.
```
abr = ABR(1, None, None)
for i in range(2, 7):
    abr.insérer(i)
```
Corriger l’ordre d’insertion afin d’obtenir un arbre complet.

3.3 Intérêt des arbres binaires de recherche

Le caractère trié d’un arbre binaire de recherche permet des opérations rapides pour rechercher une clé, ce que nous verrons dans la partie algorithmique.

Application

Comparer le nombre d’opérations nécessaires à la recherche de l’élément 15 dans l’arbre ci-dessus:
- par une méthode brutale (brute force): on itère sur tous les éléments de l’arbre par exemple avec un parcours en largeur.
- par une méthode dichotomique utilisant le fait que l’arbre binaire de recherche est « trié ».
Donner la complexité des deux méthodes pour un arbre de taille $n$ .