Chapitre 6: Circuits combinatoires*

Programme

Contenus	Capacités attendues	Commentaires
Modèle d’architecture séquentielle (von Neumann)		Les circuits combinatoires réalisent des fonctions booléennes.

L’invention du transistor en 1947 a ouvert l’ère de l’électronique pour l’humanité et a permis à l’informatique de se miniaturiser et de se démocratiser au grand public.

Nous allons voir maintenant, comment il est possible de réaliser des opérations logiques à l’aide de transistors. En effet, chaque processeur possède dans son jeu d’instructions des opérations booléennes (ou opérations bit à bit).

Il existe des transistors de diverses technologies, pour plus de simplicité, nous étudierons dans ce chapitre qu’un seul type de transistor: les transistors N-Mos. Dont voici le symbole électrique

Symbole électrique du transistor CMOS-N

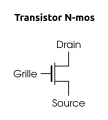
Un transistor CMOS-N possèdent trois bornes nommées:

• La grille G qui commande le fonctionnement du transistor,
• Le drain D,
• et la source S.

Une simulation de ce type de transistor est disponible en suivant ce lien: http://www.falstad.com/circuit/e-nmosfet.html

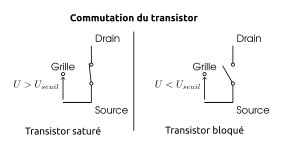
1 Commutation du transistor

Pour réaliser des circuits logiques, nous utilisons le transistor en interrupteur commandé.

En fonction de la tension appliquée entre la grille et la source $U_{GS}$, le dipôle entre le drain et la source se comporte soit comme un interrupteur ouvert soit comme un interrupteur fermé.

En plus: En plus

La résistance entre le Drain et la Source dépend fortement de la tension appliquée entre la grille et la source: $U_{GS}$, c’est une particularité des matériaux semi-conducteurs utilisés dans les transistors.

By Saumitra R Mehrotra & Gerhard Klimeck, modified by Zephyris - Own work, Public Domain, Link

Dans cette simulation, la tension de seuil se situe aux alentours de 0,45V, si bien que si:

• $U_{GS} < 0,45 V$: $R_{DS} +$, l’interrupteur commandé est ouvert.
• $U_{GS} > 0,45 V$: $R_{DS} $, l’interrupteur commandé est fermé.

En utilisant des tensions de commandes $U_{GS}$ n’ayant que deux valeurs: 0, ou 5V, il est possible d’utiliser le transistor comme un interrupteur placé entre les bornes $D$ et $S$ et commandé par la tension $U_{GS}$.

Commutation du transistor CmosN

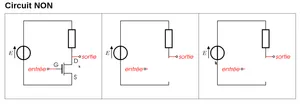
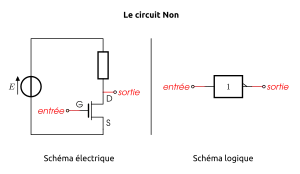
2 Réalisation d’une porte NON(NOT)

La fonction booléenne non(x) associe à une valeur booléenne $x$ son “contraire”.

Sa table de vérité est:

x	non(x)
0	1
1	0

Porte Non

Application: Schémas équivalents

1. Réaliser les deux schémas équivalents au circuit pour $U_{GS} = 0V$ et $U_{GS} = 5V$ en remplaçant le transistor par un interrupteur. 2. Vérifier que le circuit réalise bien la fonction booléenne $sortie=NON(entrée)$. On rappelle que la tension aux bornes d’un fil(ou d’un interrupteur fermé) est nulle, et la tension aux bornes d’une résistance suit la loi d’Ohm: $U=RI$.

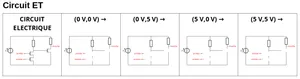
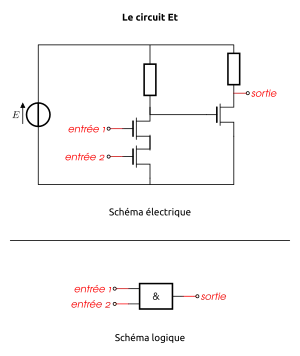
3 Réalisation d’une porte ET(AND)

La fonction booléenne et(x, y) a la table de vérité suivante:

x	y	et(x,y)
0	0	0
0	1	0
1	0	0
1	1	1

Porte Et

Application: Schémas équivalents

1. Réaliser les quatre schémas équivalents pour les couples de tensions d’entrée $(e_1, e_2) \in \left\lbrace (0V, 0V), (0V, 5V), (5V, 0V), (5V, 5V)\right\rbrace$ au circuit en remplaçant les transistors par des interrupteurs. 2.Vérifier que le circuit réalise bien la fonction booléenne $sortie=ET(entrée 1, entrée 2)$.

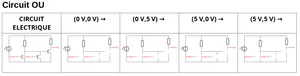
4 Réalisation d’une porte OU(OR)

La fonction booléenne $ou(x, y)$ a la table de vérité suivante:

x	y	ou(x,y)
0	0	0
0	1	1
1	0	1
1	1	1

Porte Ou

Application: Schémas équivalents

1. Réaliser les quatre schémas équivalents pour les couples de tensions d’entrée $(e_1, e_2) \in \left\lbrace (0V, 0V), (0V, 5V), (5V, 0V), (5V, 5V)\right\rbrace$au circuit en remplaçant les transistors par des interrupteurs. 2.Vérifier que le circuit réalise bien la fonction booléenne $sortie=OU(entrée 1, entrée 2)$.

5 Autres portes booléennes

5.1 La porte NON-ET(NAND)

Table de vérité

x	y	nand(x,y)
0	0	1
0	1	1
1	0	1
1	1	0

Schématisation

Porte NAND

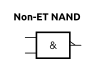
5.2 La porte NON-OU (nor)

Table de vérité

x	y	nor(x,y)
0	0	1
0	1	0
1	0	0
1	1	0

Schématisation

Porte NOR

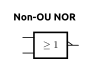
5.3 La porte OU eXclusif (xor)

Table de vérité

x	y	xor(x,y)
0	0	0
0	1	1
1	0	1
1	1	0

Schématisation

Porte XOR

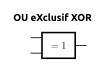
5.4 La porte ET inclusif (xnor)

Table de vérité

x	y	xnor(x,y)
0	0	1
0	1	0
1	0	0
1	1	1

Schématisation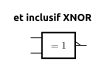

• Chapitre 13. Les Portes booléennes Informatique et sciences du numérique Spécialité ISN en terminale S - Avec des exercices corrigés et des idées de projets par Gilles Dowek