Chapitre 2: Usages avancés des tableaux

Programme

Contenus	Capacités attendues	Commentaires
Tableau indexé, tableau donné en compréhension	Lire et modifier les éléments d’un tableau grâce à leurs index. Construire un tableau par compréhension. Utiliser des tableaux de tableaux pour représenter des matrices, notation a[i][j] Itérer sur les éléments d’un tableau.	Seuls les tableaux dont les éléments sont du même type sont présentés. Aucune connaissance des tranches (slices) n’est exigible. L’aspect dynamique des tableaux de Python n’est pas évoqué. Python identifie listes et tableaux. Il n’est pas fait référence aux tableaux de la bibliothèque NumPy.

Nous nous intéressons dans ce chapitre à quelques fonctions avancées des tableaux comme leur création par compréhension et l’utilisation de tableaux de tableaux pour représenter des données à deux dimensions comme une image par exemple.

Un tableau (dynamique) possède une taille varaiable, et on peut lui ajouter ou lui enlever des éléments après sa création et son stockage en mémoire.

 CC0 via Wikimedia Commons

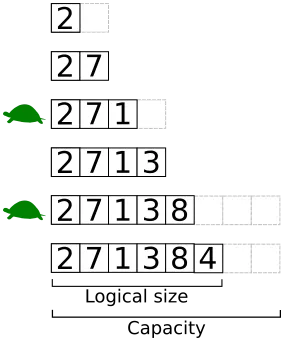
1 Tableau donné en compréhension

Plutôt que de remplir un tableau par énumération de ces éléments dans une boucle, on peut définir des listes en compréhension, c’est-à-dire des listes dont le contenu est défini par filtrage du contenu d’une autre liste.

1.1 Boucle classique

On commence par créer une liste vide, puis, on ajoute grâce à une boucle les éléments un à un à la liste grâce à la méthode append().

Voici par exemple comment créer une liste contenant les puissances de 2 de $2^1$ à $2^{12}$.

t = []
for i in range(13):
    t.append(2**i)
t

[1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096]

1.2 Écriture en compréhension

Cette construction syntaxique offre des avantages de lisibilité et de concision et se rapproche de la notation utilisée en mathématiques :

$$S=\{2^{n} | n\in {\mathbb{N}}, n<13\}$$

t = [2**n for n in range(13)]
t

[1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096]

On peut même ajouter des conditions. Par exemple ici on crée une liste des puissances de 2 des puissances paires.

t = [2**n for n in range(13) if n % 2 == 0]
t

[1, 4, 16, 64, 256, 1024, 4096]

En plus: Syntaxe complète avec `else`

Il est possible d’utiliser une clause else dans les conditions grâce à l’opérateur ternaire: valeur_si_vrai if condition else valeur_si_faux

[f(x) if condition else g(x) for x in sequence]

Par exemple:

[str(i) + " est pair" if i % 2 == 0 else str(i) + " est impair" for i in range(5)]

renvoie: ['0 est pair', '1 est impair', '2 est pair', '3 est impair', '4 est pair']

2 Tableaux à deux dimensions: les matrices

Pour représenter un tableau de données, on peut utiliser une liste de liste. $$\begin{pmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{pmatrix}$$

Stockage d'un tableau dans une liste de listes.

 Public domain via Wikimedia Commons

mat = [[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]]
mat

[[1, 2, 3], [4, 5, 6], [7, 8, 9]]

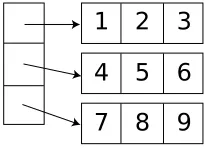
2.1 Accès aux éléments

On accède alors aux éléments en précisant l’index de ligne et de colonne: mat[i ligne][j colonne].

Par exemple pour accéder au troisième élément de la première ligne.

mat[0][2]

3

Accès au deuxième élément de la troisième ligne.

mat[2][1]

8

2.2 Accès aux lignes et colonnes

L’accès à une ligne est aisé, par exemple pour la deuxième ligne.

mat[1]

[4, 5, 6]

L’accès aux colonnes est plus délicat, on peut par exemple utiliser une liste en compréhension, par exemple pour accéder à la première colonne.

[ligne[0] for ligne in mat]

[1, 4, 7]

2.3 Itérations sur les valeurs

Comme il s’agit d’une structure imbriquée, nous devons utiliser deux boucles imbriquées.

On peut par exemple itérer sur les valeurs des lignes.

for ligne in mat:
    for val in ligne:
        print(val)

>>sortie

1
2
3
4
5
6
7
8
9