Chapitre 2: Représentation des entiers relatifs

Contenus Capacités attendues Commentaires
Représentation binaire d’un entier relatif Évaluer le nombre de bits nécessaires à l’écriture en base 2 d’un entier, de la somme ou du produit de deux nombres entiers. Utiliser le complément à 2. Il s’agit de décrire les tailles courantes des entiers (8, 16, 32 ou 64 bits). Il est possible d’évoquer la représentation des entiers de taille arbitraire de Python.

Jusqu’à maintenant, nous avons appris à représenter des entiers naturels en représentation binaire ou hexadécimale. Cependant, dans de nombreux programmes, il est nécessaire d’utiliser d’autres types de nombres comme les entiers relatifs ou les réels. Dans ce chapitre nous allons voir comment coder les nombres entiers relatifs grâce à la méthode des compléments qui permet de coder une plage symétrique d’entiers positifs et négatifs de manière à ce qu’ils puissent utiliser le même algorithme (matériel) pour l’addition sur toute la plage.

Complément à 2 sur 3 bits.

1 Méthode naïve: utilisation d’un bit de signe

La façon la plus simple de procéder serait de réserver le bit de poids fort pour le signe(0 pour positif et 1 pour négatif), et de garder le rester pour la représentation de la valeur absolue du nombre.

Avec un codage utilisant des mots de n bits, on pourrait représenter des nombres entre −2n−1+1-2^{n-1}+1 et 2n−1−12^{n-1}-1.

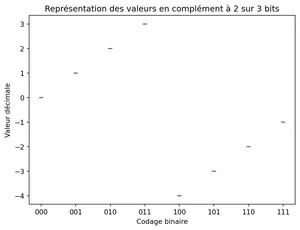
Par exemple, avec un codage sur 3 bits, des nombres entre -3 et 3:

Représentation binaire Valeur décimale
000 +0
001 +1
010 +2
011 +3
100 -0
101 -1
110 -2
111 -3

Malheureusement cette représentation possède deux inconvénients. Le premier (mineur) est que le nombre zéro (0) possède deux représentations. L’autre inconvénient (majeur) est que cette représentation impose de modifier l’algorithme d’addition ; si un des nombres est négatif, l’addition binaire usuelle donne un résultat incorrect. Voir l’article de Wikipédia pour plus de détails

Vérifier que 3 - 2 ne donne pas le bon résultat avec cet encodage en binaire.

2 Notation en complément à deux

Cette méthode permet de remédier aux problèmes évoqués ci-dessus.

On utilise un encodage de longueur fixe nn:

  • La première moitié représente les entiers positifs ou nul codés normalement avec un 0 sur le bit de poids fort;
  • La deuxième moitié représente les entiers strictement négatifs. Pour cela on leur ajoute 2n2^n et on retrouve un 1 sur le bit de poids fort.
Note

Dans cet encodage, le bit de poids fort contient encore l’information du signe:

  • 0 pour les entiers positifs ou nul.
  • 1 pour les entiers strictement négatifs.

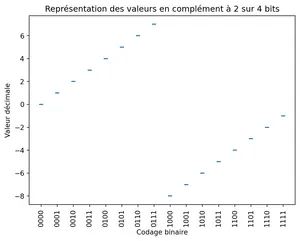
En complément à 2 sur nn bits, on peut représenter des nombres entre −2n−1-2^{n-1} et 2n−1−12^{n-1}-1.

2.1 Méthode d’encodage

L’entier négatif xx est codé comme s’il s’agissait de l’entier x+2nx + 2^{n} ou n est la taille du mot.

Il est possible d’appliquer un algorithme simple pour réaliser cette addition en binaire (cette méthode sera désignée comme 2ᵉ méthode par la suite).

  • On inverse les bits de l’écriture binaire de sa valeur absolue.
  • On ajoute 1 au résultat (les dépassements sont ignorés).

Article Wikipédia sur le complément à deux

Utilisons cet encodage sur 3 bits.

−110=?2 -1_{10} = ?_{2}

2.1.0.1 1ère méthode

−1=>−1+23=710=1112 -1 => -1 + 2^3 = 7_{10} = 111_2

2.1.0.2 2e méthode
  1. La valeur −1-1 a pour valeur absolue 11 codé 001 sur 3 bits.
  2. On inverse les bits: 110
  3. On ajoute 1: 111

Les deux méthodes donnent le même résultat:

−110=1112 -1_{10} = 111_{2}

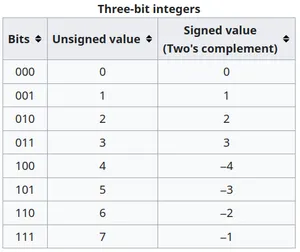
2.1.1 Tableau de valeurs

Avec un codage sur 3 bits, on peut coder des nombres entre −23−1=−4-2^{3-1}=-4 et −23−1−1=3-2^{3-1}-1=3.

Représentation binaire Valeur décimale
000 +0
001 +1
010 +2
011 +3
100 -4
101 -3
110 -2
111 -1

2.2 Méthode de décodage

Pour connaitre le nombre que représente un entier négatif, on effectue la démarche inverse:

  • On lui retranche 1 puis,
  • on inverse tous ces bits,
  • On convertit en base 10, et on ajoute le signe -.

Ce qui revient à lui soustraire 2n2^n.

Toujours en travaillant sur 3 bits:

1102=?10 110_2 = ?_{10}

2.2.1 1ère méthode

1102=610=>6−23=−210 110_2 = 6_{10} => 6 - 2^3 = -2_{10}

2.2.2 2e méthode

  1. On retranche 1: 110 - 1 = 101
  2. On inverse les bits: 010
  3. On convertit en base 10: 0102=210010_2 = 2_{10} donc c’est −2-2.

Les deux méthodes donnent le même résultat:

1102=−210 110_2 = -2_{10}

3 Opérations

Astuce

Il faut bien garder à l’esprit que l’encodage en complément à deux ne peut être fait que sur des mots binaires de taille fixe et que les dépassements de capacité ne sont pas pris en compte.

3.1 Soustraction

Réalisons le calcul 3−2=3+(−2)3-2 = 3+ (-2) sur trois bits.

   011
  +110
  ----
(1)001

On trouve bien 0012=1{001}_2=1 car le 4e bit n’est pas prise en compte.

3.2 Multiplication

Réalisons le calcul 2*(−2)2*(-2) sur trois bits.

     010
    x110
    ----
     000
    010
   010
   -----
 (01)100

On trouve bien sur trois bits 1002=−4{100}_2=-4.